Integrals!

Introduction

Integrals are perhaps my favorite part of math—at least so far. They are applicable in so many ways, and are fun to do!

So, let's explain the concepts

On this page, I'm only going to go over the basic techniques of integration. There are some more for definite integrals, but they're a lot more difficult to teach are more of an intuition thing, along with some time playing around with the integral.

Assuming nothing

I hope to make this approachable for anyone, so I'm going to assume you know nothing about integration, not even what it means. So, let's start with the definition of an integral. An integral is the signed area under a curve. That may feel somewhat jargony, but hopefully this example can help illuminate you.

The first time I truly understood integrals was in physics, seeing the physical manifestation of the integral. Let's have a constant velocity object, moving at 5 m/s, starting at position 0.

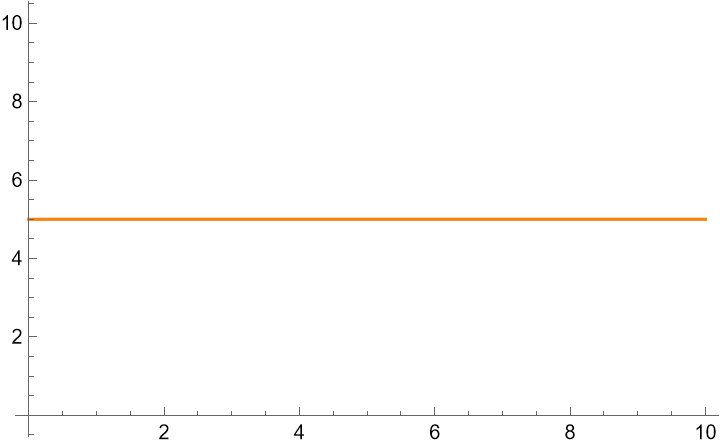
If you know that the object is moving at 5 m/s, you can easily calculate it's position. Distance is equal to speed times time, so the position is 5 meters per second times the time. So, at 1 second, the position is 5 meters. At 2 seconds, the position is 10 meters. At 3 seconds, the position is 15 meters. And so on.

Recall how multiplication was portrayed in elementary school. You had two numbers, and you would draw a rectangle between them. So, 2x3 would be a rectangle with a width of 2 and a height of 3. The area of the rectangle is 6, and so 2x3 is 6. We can do the same here, but we can also parameterize the rectangle with time.

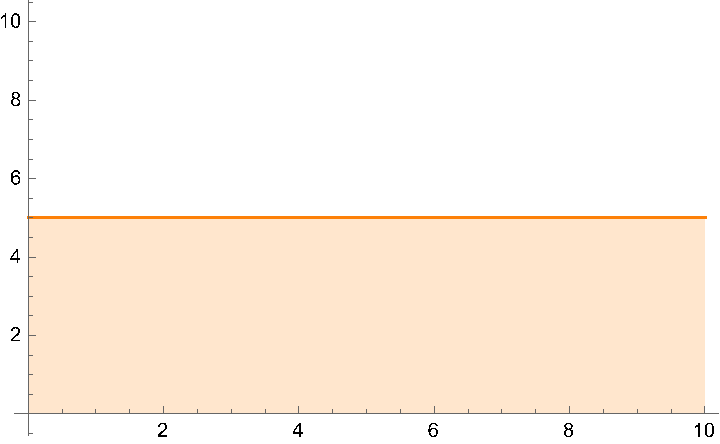
So the equation will be 5 m/s × t, where t is the time. (The area of the rectangle is the integral of the function, so you found your first integral.) This makes sense, because when you multiply meters per second by a number of seconds, you will just get meters out. The units check out, and the formula also matches what we believed beforehand. If we call the function that graphs the position of the object as f(t), f(t) = 5, and the integral, where t starts at 0, is F(t) = 5t.

Bringing it up a notch

We now know that the integral of a constant is that constant times the variable. But this time we were given the initial starting condition. If we didn't know the starting position, we would have to add a constant to show our uncertainty about the position. When subtracting two results from equations, the constants would cancel, but if you need the definite position at a time we wouldn't know.

Let's write down what we've learned so far, using the syntax of math. ∫a ⅆx = a × x + c₁, where a is a constant, x is the variable, and c₁ is the constant. This is the integral of a constant. Now, let's make sense of the syntax. The integral sign is ∫, and the ⅆx signifies that the variable to integrate with respect to is x.

The previous example was f(t) = 5. Writing it in the mathy way, it would be F(t) = ∫5 ⅆt = 5t + c₁. We know F(0) = 0, so using that we can solve for c₁. F(0) = 0 = 5 × 0 + c₁, therefore 0 = c₁, therefore F(t) = 5t. This is the same as what we found before using the rectangle method.

Unfortunately, we can't always use the rectangle method. Sometimes, the function is not a constant. To do this for more complicated integrals we need to take a trip through derivatives. But, since were building this from the ground up, I won't assume you know derivatives. So, let's start with the simplest form of them.

Fundamental Theories

Derivatives

At the moment, we don't care about derivatives for their actual purpose, but into order to explain their connection to integrals, I unfortunately will have to explain them, their purpose, and how some derivatives are defined and proven.

Once again, we return to the graphs. The derivative of a function is the slope of the tangent line at a point. Below is the graph f(x) = x.

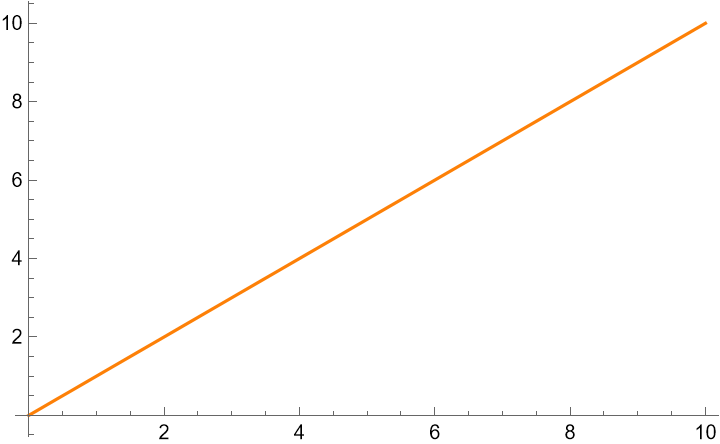
As you know from a math class (probably algebra 1), the slope of the line in the form f(x) = ax + b is a. So, the derivative of f(x) = x is 1 (a = 1, b = 0). But we can extend this notion of slope to more than just lines. We can take the derivative at a point, on any curve.

We do so by drawing a line across a smaller and smaller area of the curve. The slope of the resulting line is the derivative at that point. See an example for f(x) = x² below.

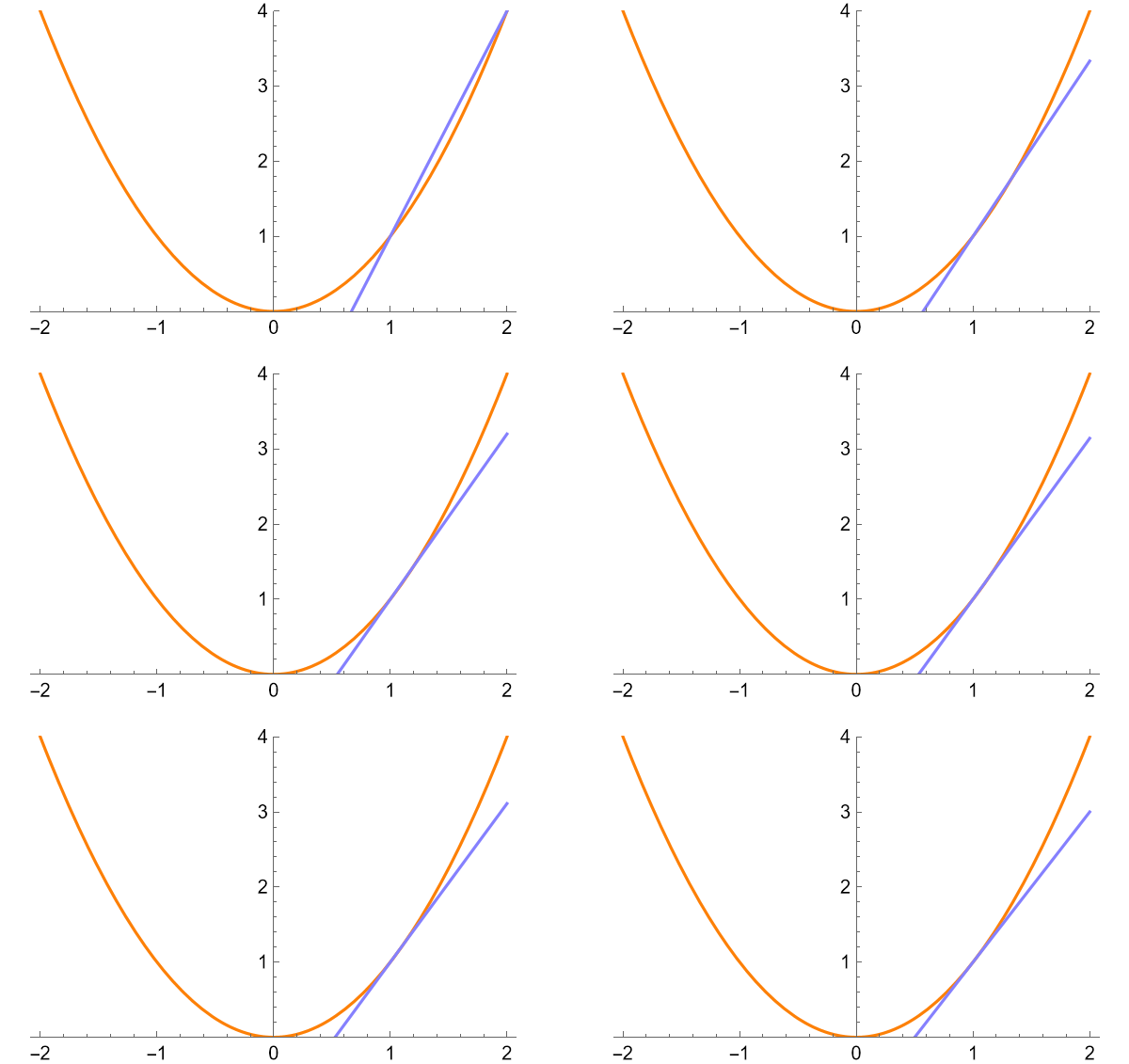
The slope of the final line, with sample points infinitely close together is the derivative at that point. The slope of line is 2, therefore the derivative of f(x) at x = 1 is 2.

This is a good intuitive basis for the formal definition of the derivative. Let's think about what we were doing when getting slopes. The slope was (y₂ - y₁) / (x₂ - x₁), where x₁ = 1, y₁ = f(1) = 1, x₂ = 1 + h, and y₂ = f(1 + h), where h is a distance away from the initial point. (When plotting the line, I used h = { 1, 1/3, 1/5, 1/7, 1/9, 1/∞ }.), Plug in to get (f(1 + h) - f(1)) / (1 + h - 1), which is the general definition of the derivative at x = 1, as h→0.

The general form of that for any is (f(x + h) - f(x)) / (x + h - x), and we can cancel the x's on the bottom to get (f(x + h) - f(x)) / h, which equals f'(x) as h→0. This is the formal definition of the derivative.

Mathematicians formally write "as h→0" as a limit, like in this case: f'(x) = lim h→0 (f(x + h) - f(x)) / h, which is exactly what you would see in textbooks.

The chain rule

This is the most important rule for derivatives. With in, you can find the derivative of any function and solve for the other rules of derivatives. The chain rule is the following: if f(x) = g(j(x)), then f'(x) = j'(x)g'(j(x)). But don't just take my word for it: let's prove it using the definition of the derivative.

f(x) = g(j(x)) therefore f'(x) = lim h→0 (g(j(x + h)) - g(j(x))) / h

Multiply by 1 = (j(x + h) - j(x))/(j(x + h) - j(x)):
f'(x) = lim h→0 ((g(j(x + h)) - g(j(x))) / h)((j(x + h) - j(x))/(j(x + h) - j(x)))

Swap the denominators:
f'(x) = lim h→0 ((g(j(x + h)) - g(j(x))) / (j(x + h) - j(x)))((j(x + h) - j(x))/h)

Split the limit via the product property:
f'(x) = lim h→0 ((g(j(x + h)) - g(j(x))) / (j(x + h) - j(x))) lim h→0 ((j(x + h) - j(x))/h)

Via the definition of the derivative, lim h→0 (j(x + h) - j(x))/h = j'(x), so:
f'(x) = lim h→0 ((g(j(x + h)) - g(j(x))) / (j(x + h) - j(x)))j'(x)

Rearrange:
f'(x) = j'(x) lim h→0 ((g(j(x + h)) - g(j(x))) / (j(x + h) - j(x)))

We need to redefine our variables. u = j(x + h) - j(x), therefore j(x) + u = j(x + h). We also need to find what happens near h = 0. As you can see here, if h = 0, u = j(x) - j(x) = 0, so h→0 means u→0.
f'(x) = j'(x) lim h→0 ((g(j(x) + u) - g(j(x))) / u

We set s = j(x):
f'(x) = j'(x) lim h→0 ((g(s + u) - g(s)) / u

Apply the definition of the derivative:
f'(x) = j'(x) g'(s)

Substitute variable in:
f'(x) = j'(x)g'(j(x))

And we're done! This is the chain rule. This is a good start to our toolbox, but to use it for integrals, we need to show how integrals and derivatives are connected.

Proving the mean value theorem for integrals

This may seem unrelated, but it's necessary to prove the fundamental theorem of calculus.

We have a function f(x), and it is continuous on the interval [a, b]. On this interval there is a x-value d such that f(d) is a absolute maximum value of f(x) on the interval, and another x-value k such that f(k) is a absolute minimum value of f(x) on the interval. Given this, V, the value of the integral ∫_a^b f(x) ⅆx is f(k)(b - a) < V < f(d)(b - a). This is done by drawing rectangles from x = a to x = b, and heights d and k.

Because the function f(x) is continuous, every value between f(k) and f(d) is also a value of f(x) on the interval [a, b]. Therefore, for some c on the interval [a, b], V = f(c)(b - a).

Fundamental Theorem of Calculus

The fundamental theorem of calculus is if f(x) is continuous on [a,b], then the derivative with respect to x of the integral of f(t) with respect to t from a to x is f(x).

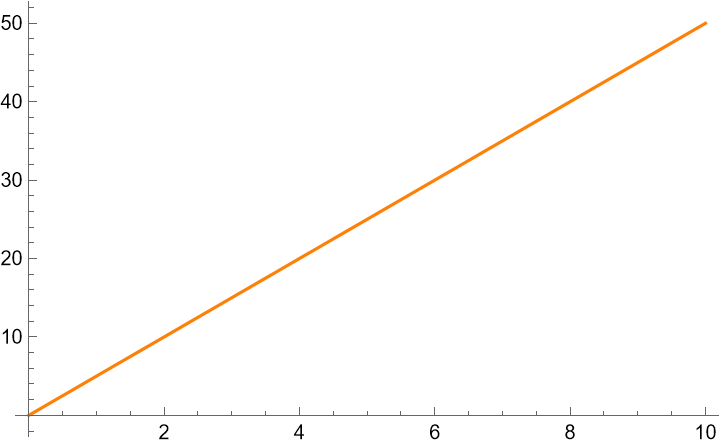
Unlike the chain rule, this can be explained easily as well as proven. Let us return the physics example. Here is the plot of our position, F(t) = 5t.

We already showed how to get here from the plot of velocity, f(t) = 5, by integrating, but how can we go backwards? We should read into the formula given more. F(t) = 5t means that for every 1 second of time, the position increases by 5 meters. This is the same as saying that velocity is 5 m/s at every second, and we have just gone backwards in this specfic case.

More generally, to find the velocity at a certain time, we should look at the slope. Velocity is the rate of change of position, so the slope at a time is the same as the velocity at that time.

Now to prove this principle.
F(x) = ∫_a^x f(t) ⅆt

Duplicate the integral to F(x) and F(x + h):
F(x) = ∫_a^x f(t) ⅆt
F(x + h) = ∫_a^{x + h} f(t) ⅆt

Subtract the integrals:
F(x) - F(x + h) = ∫_a^x f(t) ⅆt - ∫_a^{x + h} f(t) ⅆt

Split integral from a to x + h into two integrals from a to x and x to x + h:
F(x) - F(x + h) = ∫_a^x f(t) ⅆt - (∫_a^x f(t) ⅆt + ∫_x^{x + h} f(t) ⅆt)

Distribute negative sign:
F(x) - F(x + h) = ∫_a^x f(t) ⅆt - ∫_a^x f(t) ⅆt - ∫_x^{x + h} f(t) ⅆt

Cancel integrals ∫_a^x f(t) ⅆt:
F(x) - F(x + h) = - ∫_x^{x + h} f(t) ⅆt

Multiply both sides by -1:
F(x + h) - F(x) = ∫_x^{x + h} f(t) ⅆt

Apply the Mean Value Theorem for Integrals (this requires f(x) be continuous):
c is on the interval [x, x+ h]
F(x + h) - F(x) = f(c)(x + h - x)

Simplify:
F(x + h) - F(x) = f(c)h

Divide both sides by h:
(F(x + h) - F(x)) / h = f(c)

Take the limit as h approaches 0:
lim h→0 (F(x + h) - F(x)) / h = lim h→0 f(c)

Apply the definition of the derivative:
F'(x) = lim h→0 f(c)

Recall that c is on the interval [x, x + h]. If h = 0, this means that the interval collapses to [x, x], or just x.
F'(x) = f(x)

This is the main meat of the result. The derivative of an integral is the function that was integrated.

Corollary

If F(x) = ∫_a^x f(t) ⅆt, for any a, then ∫_a^b f(x) ⅆx = F(b) - F(a)

Prove it!:
F(x) = ∫_a^x f(t) ⅆt, for any a.
G(x) = ∫_b^x f(t) ⅆt, for any b.

Via the first part of the theorem, we know that F'(x) = f(x).
F'(x) = f(x)
G'(x) = f(x)

If the derivatives of two function are the same, they can only differ by a constant.
F(x) + c = G(x) = ∫_b^x f(t) ⅆt, for any b.

Plug in x = b:
F(b) + c = G(b) = ∫_b^b f(t) ⅆt, for any b.

An integral from b to b is always zero. You cannot have area if there is no width:
F(b) + c = G(b) = 0

Reformat:
F(b) + c = 0
c = -F(b)

Plug c = -F(b) into F(x) + c = G(x) = ∫_b^x f(t) ⅆt, for any b:
F(x) - F(b) = G(x) = ∫_b^x f(t) ⅆt, for any b.

Rename some variables (x→b, b→a):
F(b) - F(a) = G(b) = ∫_a^b f(t) ⅆt
F(b) - F(a) = ∫_a^b f(t) ⅆt

Proven!

Less fundamental, but still important, theories

Let's do some stuff with the fundamental theroems we just proved.

The derivative of ln(x)

First we need to define what ln(x) is. I will define it as the inverse of the exponential function, e^x. Therefore, ln(e^x) = x and e^ln(x) = x. Furthermore, the definition of e is that if f(x) = e^x, f'(x) = e^x. Through use of L'Hopital's rule you can show that this is equivalent to the other definition of e, that e = lim n→∞ (1 + 1/n)ⁿ, but that is left as an exercise for the reader.

f(x) = ln(x)
e^f(x) = e^ln(x)
e^f(x) = x

Apply the chain rule to the left where g(x) = e^x and j(x) = f(x) and knowledge of the slope of linear functions to the right:
f'(x) e^f(x) = 1

Recall e^f(x) = x
f'(x) x = 1
f'(x) = 1 / x

Therefore, the derivative of ln(x) is 1 / x.

Proving that the sum of derivatives is the same as the derivative of the sum

Proving f(x) = h(x) + g(x) implies f'(x) = h'(x) + g'(x).

f(x) = h(x) + g(x)

Apply the definition of the derivative: f'(x) = lim h→0 (f(x + h) - f(x)) / h
f'(x) = lim h→0 ((h(x + h) + g(x + h)) - (h(x) + g(x))) / h
f'(x) = lim h→0 (h(x + h) - h(x) + g(x + h) - g(x)) / h

Split limit:
f'(x) = lim h→0 (h(x + h) - h(x)) / h + lim h→0 (g(x + h) - g(x)) / h

Each limit is the definition of the derivative:
f'(x) = h'(x) + g'(x)

Proven!

Proving that constants on a function multiply the derivative

f(x) = a g(x)
ln(f(x)) = ln(a g(x))
ln(f(x)) = ln(a) + ln(g(x))

Use the chain rule to find the derivative of ln(f(x)) and ln(g(x)), and the derivative of a constant is zero (a x + b ⇒ a):
f'(x) × 1 / f(x) = 0 + g'(x) × 1 / g(x)
f'(x) / f(x) = g'(x) / g(x)

Replace f(x) with a g(x):
f'(x) / (a g(x)) = g'(x) / g(x)

Multiply both sides by a g(x):
f'(x) = a g'(x)

Proving the power rule

f(x) = xⁿ
ln(f(x)) = ln(xⁿ)
ln(f(x)) = n ln(x)

Take the derivative of both sides, using the chain rule on the left:
f'(x) × 1 / f(x) = n × 1 / x
f'(x) / f(x) = n / x

Replace f(x) with xⁿ:
f'(x) / xⁿ = n / x

Multiply both sides by xⁿ:
f'(x) = n x^{n - 1}

Proving the product rule

f(x) = g(x) h(x)
ln(f(x)) = ln(g(x) h(x))
ln(f(x)) = ln(g(x)) + ln(h(x))

Use the chain rule to find the derivative of ln(f(x)), ln(g(x)), and ln(h(x)):
f'(x) × 1 / f(x) = g'(xruel) × 1 / g(x) + h'(x) × 1 / h(x)
f'(x) / f(x) = g'(x) / g(x) + h'(x) / h(x)

Replace f(x) with g(x) h(x):
f'(x) / (g(x) h(x)) = g'(x) / g(x) + h'(x) / h(x)

Multiply both sides by g(x) h(x):
f'(x) = g'(x) h(x) + g(x) h'(x)

Derivatives of exponentials

f(x) = a^x
ln(f(x)) = ln(a^x)
ln(f(x)) = x ln(a)

Take the derivative of both sides, using the chain rule on the left:
f'(x) × 1 / f(x) = ln(a)
f'(x) / f(x) = ln(a)

Replace f(x) with a^x:
f'(x) / a^x = ln(a)

Multiply both sides by a^x:
f'(x) = ln(a) a^x

Quotient Rule

Returning to integration

With all these tools under our belt, lets prove some things about integrals now. We can start by proving the power rule for integrals.

Proving the power rule for integrals

∫ xⁿ ⅆx = x^{n + 1} / (n + 1) + c₁ is the formula for the power rule, but how did we get there?

Set F(x) = x^{n + 1} / (n + 1).

F'(x) via the power rule is F'(x) = (n + 1) x^{(n + 1 - 1)} / (n + 1)

Simplify:
F'(x) = xⁿ

Via the fundamental theorem of calculus, F'(x) = f(x).
f(x) = xⁿ ⇒ F(x) = ∫ xⁿ ⅆx

This mean a possible integral for xⁿ is x^(n + 1) / (n + 1). To access all the possible integrals, add a constant.

Therefore, ∫ xⁿ ⅆx = x^{n + 1} / (n + 1) + c₁

u-substitution

F(u) = ∫ f(u) ⅆu
F is a antiderivative of f.

Set g(x) = F(h(x)).
By the chain rule g'(x) = h'(x)F'(h(x)) = h'(x)f(h(x))
Therefore, F(h(x)) is an answer to ∫ h'(x)f(h(x)) ⅆx.

This means that the general form is ∫ h'(x)f(h(x)) ⅆx = F(h(x)) + c₁. This is the form that u-sub takes, although generally its worded differently.

Let's do an example. ∫ 2x e^x2 ⅆx.

Set h(x) = x², therefore, h'(x) = 2x, by the power rule and set f(x) = e^x.

Therefore, ∫ 2x e^x2 ⅆx. = ∫ h'(x) e^h(x) ⅆx = ∫ h'(x)f(h(x)) ⅆx

Apply the rule we just learned: ∫ h'(x)f(h(x)) ⅆx = F(h(x)) + c₁
We do first need to find what F(x) is.

F(x) = ∫ e^x ⅆx = e^x + c₂

Plug F(x) into the result F(h(x)) + c₁:
e^h(x) + c₂ + c₁

Combine constants:
e^h(x) + c₃
Rename it to c₁ because it's the only constant remaining:
e^h(x) + c₁

Plug in h(x):
e^x2 + c₁

This is doing the process of u-substitution, but it is generally easier to do it another way, and hopefully you can see where the parallels are.

The easier way

Here is the example. ∫ 2x e^x2 ⅆx.
Set u = x². Therefore, ⅆu = 2x ⅆx.

Solve for ⅆx:
ⅆx = ⅆu / 2x

Plug ⅆu / 2x into the integral and make the u-sub:
∫ 2x e^u ⅆu / 2x

Cancel the 2x's:
∫ e^u ⅆu
∫ e^u ⅆu = e^u + c₁

Substitute u for x²:
e^x2 + c₁

This is the same thing, but it far easier to do on larger integrals.

Integrals of exponentials

∫ a^x ⅆx

Rewrite a^x:
∫ e^ln(a)x ⅆx

Use u-sub:
u = ln(a)x
ⅆu = ln(a) ⅆx
∫ e^u / ln(a) ⅆu

Pull out the 1 / ln(a) (you can pull constants out of integrals because you can out of derivatives):
1 / ln(a) × ∫ e^u ⅆu

I defined that the derivative of e^x is itself. Therefore, the integral of e^x is also itself, by the fundamental theorem of calculus.
1 / ln(a) × ∫ e^u ⅆu = 1 / ln(a) × e^u + c₁

Substitute u for ln(a)x:
1 / ln(a) × e^ln(a)x + c₁

Simplify:
a^x / ln(a) + c₁

Integration by parts

This is the last thing left to prove. Everything else is just algebraic manipulation that is esspecially useful for integrals. Integration by parts is actually isn't even bad to prove!

Start with the product rule:
(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)

Take the integral of both sides:
∫ (f(x)g(x))' ⅆx = ∫ f'(x)g(x) + f(x)g'(x) ⅆx

Apply the fundamental theorem of calculus:
f(x)g(x) = ∫ f'(x)g(x) + f(x)g'(x) ⅆx

Split sum:
f(x)g(x) = ∫ f'(x)g(x) ⅆx + ∫ f(x)g'(x) ⅆx

Rearrange terms:
f(x)g(x) - ∫ f'(x)g(x) ⅆx = ∫ f(x)g'(x) ⅆx

And that's all. Some people may

Trig substitution

Partial fractions

Other Stuff coming soon:

Differential Equations

Series